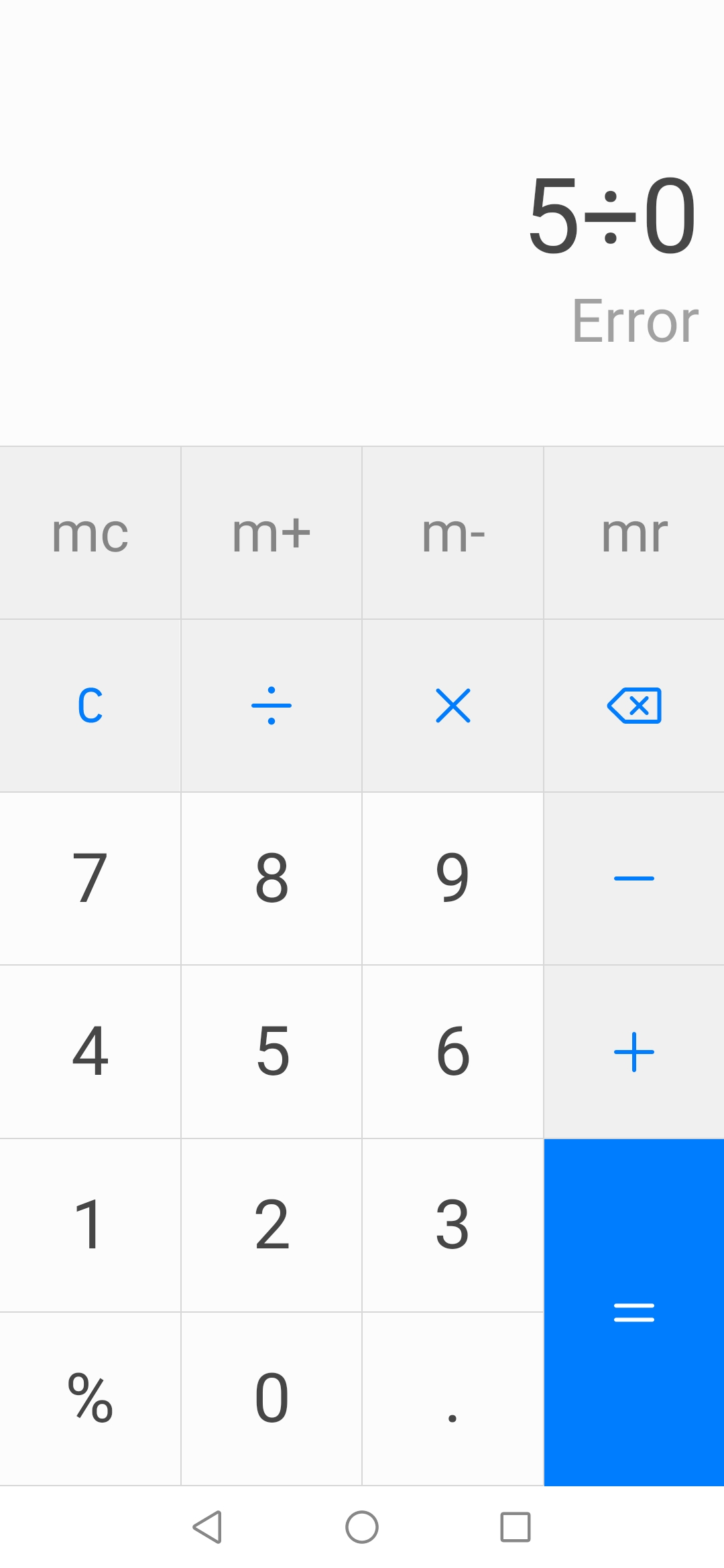
Деление на ноль является одним из основных математических запретов, которые возникают из-за самой природы чисел и операций над ними. Деление на ноль не имеет смысла и не может быть определено в числовой системе, которая работает в рамках арифметических правил. Попытка выполнить деление на ноль приводит к неопределенности и противоречиям, которые невозможно разрешить.
Деление на ноль в математической терминологии означает разбиение некоторого числа на ноль равных частей. Но если у нас нет ничего для деления, то как мы можем разделить на ноль? Попытка разбить что-то на ноль противоречит базовым принципам арифметики, таким как распределительный закон и обратная операция умножения.
Разработчики математических систем в течение истории искали способы решения этой проблемы. Однако они установили, что деление на ноль противоречит логике и не имеет математического смысла. Поэтому оно запрещено и рассматривается как операция, которая не может быть выполнена.
Почему деление на ноль невозможно и лишено смысла
Когда мы делим одно число на другое, мы ищем ответ на вопрос: сколько раз второе число «вмещается» в первое. Но что происходит, когда мы пытаемся разделить на ноль?
Представьте, что у вас есть 10 яблок, и вы хотите разделить их на 0 корзин. Каков будет результат этого деления? Мы не можем разделить яблоки на нуль корзин, потому что нуль корзин не имеют размера и не могут «вместить» яблоки.
Аналогично, в математике мы не можем разделить число на ноль, потому что нуль не имеет размера и не может быть вторым числом, которое «вмещается» в первое. Если мы представим, что деление на ноль возможно, то это приводит к противоречиям и неопределенностям в математических выражениях и уравнениях.
Кроме того, деление на ноль может привести к ошибкам и проблемам в вычислениях. Если программа или устройство пытаются выполнить деление на ноль, это может вызвать сбой или неправильный результат. Поэтому во многих программных языках и математических системах деление на ноль запрещено.
Причины, по которым нельзя делить на ноль
1. Нарушение основных принципов математики: Деление является обратной операцией умножения. Если мы разделим число на другое число, то умножив полученное частное на делитель, мы должны получить исходное число. Однако при делении на ноль этот принцип нарушается, так как умножение на ноль не позволяет восстановить исходное число.
2. Неопределенность результата: Если попытаться разделить любое число на ноль, то результат будет неопределен. Например, 6/0 не имеет определенного значения. Каждая попытка деления на ноль приводит к такой же неопределенности, потому что невозможно найти число, умножив которое на ноль, получим исходное число. Это приводит к несостоятельности алгебры.
3. Угроза для математических моделей: Математические модели часто используются для описания и прогнозирования реальных явлений. Они основаны на алгебре и арифметике, которые являются основами научного знания. Если бы допустимо было делить на ноль, то это могло бы привести к ошибочным или нелогичным результатам в математических моделях, что было бы неприемлемо для научной точности и достоверности.
4. Ненатуральный характер операции: Деление на ноль не имеет смысла и в реальной жизни. Нельзя разделить какое-либо количество предметов на ноль или поделить какую-либо сумму денег на ноль. Понятие деления на ноль не имеет физического, экономического или практического смысла.
Все эти причины объясняют, почему деление на ноль считается математической ошибкой и не имеет смысла в контексте обычной арифметики.
Деление на ноль противоречит основным арифметическим правилам
Основное правило арифметики утверждает, что при делении числа на другое число мы получаем результат, который удовлетворяет простому соотношению: делимое равно произведению делителя на частное. Однако, при попытке поделить на ноль, это правило нарушается.
Деление на ноль в своей сути является математической рекурсией, поскольку частное от деления на ноль должно рассчитываться бесконечное количество раз. Однако такая бесконечность невозможна, поскольку она не имеет конкретного значения и противоречит самой идее деления.
Кроме того, деление на ноль может приводить к неопределенностям в целых числах и дробях. Когда мы делим ненулевое число на ноль, мы получаем бесконечно большое число или минус бесконечность, в зависимости от знака числа.
С другой стороны, деление нуля на ноль не имеет смысла, поскольку оно неопределено. Мы не можем определить, какое число следует получить в результате такого деления.
Деление на ноль приводит к неопределенности и противоречиям
В математике существует классическое правило, которое говорит нам, что любое число, деленное на ноль, равно бесконечности. Однако, это правило имеет практический смысл только в определенных случаях и ситуациях. В большинстве случаев деление на ноль приводит к неопределенности, что означает, что мы ничего не можем сказать о результате такой операции.
Попытка разделить число на ноль приводит к противоречию с основными математическими законами. Например, рассмотрим утверждение: 1 = 2, и применим к нему правило деления: 1/0 = 2/0. В результате получим равенство 1 = 2, что явно противоречит математическим законам и логике.
Кроме того, деление на ноль приводит к проблемам с определением пределов и производных функций. Если мы пытаемся вычислить предел функции, содержащей деление на ноль, то получим неопределенность вида 0/0 или бесконечность/бесконечность, что делает невозможным определение значения предела.
Важно понимать, что деление на ноль является некорректной операцией. В программах и уравнениях такая операция может привести к ошибкам или некорректным результатам. Поэтому, во избежание противоречий и неопределенностей, деление на ноль следует избегать и, если возможно, заменять на другие математические операции или переформулировать задачу.
Почему деление нуля на ноль не имеет смысла
При делении числа на другое число, результат можно интерпретировать, как количество раз, которое первое число содержится во втором. Если мы делим ненулевое число на ноль, мы пытаемся найти такое число, которое при умножении на ноль даст нам исходное число. Однако, такого числа не существует, потому что любое число, умноженное на ноль, всегда будет равно нулю.
Таким образом, деление нуля на ноль не имеет определенного значения и не может быть правильно рассчитано. В математике, когда результат операции не имеет определенного значения, он считается «неопределенным».
Если мы разделим ноль на ноль, ситуация становится еще более сложной. Мы пытаемся найти число, которое при умножении на ноль даст нам ноль. Однако, поскольку любое число, умноженное на ноль, всегда будет равно нулю, мы не можем определить единственный результат для этой операции. Различные значения могут быть справедливыми, и, следовательно, деление нуля на ноль бессмысленно и не имеет определенного результата.
Математические выражения с делением нуля на ноль называются «недопустимыми». Они представляют собой особые случаи, которые не могут быть вычислены с использованием обычных правил математики. Для обработки таких случаев математики используют пределы и другие концепции, которые позволяют лучше понять поведение функций в окрестности точек, включая недопустимые значения.
Ноль является «нейтральным» элементом в арифметике
В сложении ноль действует как идентитет, то есть прибавление нуля к числу не меняет его: a + 0 = a.
В вычитании, ноль действует как обратная операция к самому себе: a - 0 = a. Это объясняется тем, что вычитание нуля не меняет исходного значения числа.
Умножение на ноль приводит к тому, что любое число становится нулём: a * 0 = 0. Число никаким образом не влияет на результат умножения.
Однако деление на ноль не имеет определенного значения. Это связано с тем, что деление определяет, сколько раз одно число содержится в другом числе. Если ноль является делителем, то мы хотим разделить какое-то число на «ничто», что не имеет логического смысла.
Также в случае деления нуля на ноль, мы хотим узнать, сколько раз ноль содержится в ноль. Но такое число не существует, так как деление на ноль не имеет определенного значения.
Есть несколько подходов к математическому определению деления на ноль, но все они приводят к противоречиям или неопределённости. Поэтому, чтобы избежать неприятностей и сохранить систему арифметики в целом разделимость на ноль запрещена.
Деление нуля на ноль противоречит определению деления
Если мы попытаемся разделить ноль на ноль, то получим ситуацию, когда неизвестно, какое число нужно умножить на ноль, чтобы получить ноль. Для любого числа c обычно выполняется равенство 0 * c = 0, но когда речь идет о делении нуля на ноль, нет ни одного числа, которое удовлетворяло бы этому условию.
Поэтому, деление нуля на ноль не имеет смысла и является неопределенным действием. В математике нельзя просто взять и поделить ноль на ноль, потому что такие операции не имеют однозначного результата и нарушают определение деления.
Нужно помнить, что деление нуля на ноль является ошибкой и не имеет смысла в математических вычислениях. Это важное правило, которое следует соблюдать, чтобы избежать противоречий и некорректных результатов в вычислениях.
Вопрос-ответ:
Почему нельзя делить на ноль?
Нельзя делить на ноль, потому что в математике нет определения для такой операции. При делении числа на ноль получается бесконечность или неопределенность, что противоречит основным принципам математики.
Почему деление нуля на ноль не имеет смысла?
Деление нуля на ноль не имеет смысла, потому что нет однозначного значения, которое можно было бы получить в результате этой операции. Ноль разделенный на ноль может быть равен любому числу, так как ноль может быть результатом умножения любого числа на ноль.
Какие проблемы могут возникнуть при делении на ноль?
При делении на ноль могут возникать различные проблемы. Например, в компьютерных программах деление на ноль может вызывать ошибки и сбои. В научных расчетах и инженерных задачах деление на ноль может привести к непредсказуемым результатам и искаженным данным.
Можно ли как-то определить результат деления нуля на ноль?
Нет, нельзя однозначно определить результат деления нуля на ноль. Это связано с тем, что при такой операции получается неопределенность. В математике можно работать с пределами и асимптотами, которые приближаются к бесконечности или другим значениям, но это не является строгим определением результата такого деления.
Почему в некоторых программных языках разрешается деление на ноль?
В некоторых программных языках разрешается деление на ноль, чтобы предоставить программистам большую гибкость и управление ошибками. Однако, при делении на ноль в таких языках может возникать ошибка или возвращаться специальное значение, которое указывает на неопределенность или бесконечность.
Почему нельзя делить на ноль?
Деление на ноль не определено в математике. При попытке деления на ноль возникают различные противоречия и неопределенности, поэтому это операция запрещена.